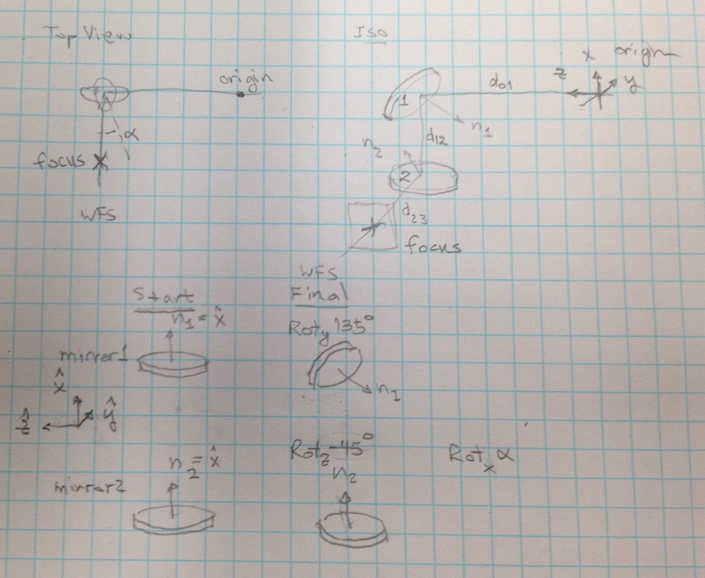Wavefront Sensor Field Steering

Top-Level Use

Field steering requires the coordinated move of two mirrors. Since there are two degrees of freedom (in each axis) there are two things that can be controlled given the appropriate decoupling function applied to the mirror motions:

• pointing where the field is moved without shifing the exit pupil, and
• centering where the pupil is moved without shifting the field

Both kinds of move may be needed during alignment, but, hopefully, the decoupling functions are well enough modeled and calibrated so that during on-sky operations only pointing moves are needed.

This module defines the decoupling functions and can generate lookup table maps or apply the functions directly during field steer operations.

To use this code to print out motor commands for certain pointing or centering moves:

from fieldSteer import *
point(x,y)
center(u,v)

The output of these calculations can be directly connected to the motor control dispatchers via the command() function, for example:

command(point(x,y))
command(center(u,v))

Note: the moves (x,y), (u,v) are absolute, because it is a nonlinear model. (x,y) are in arecseconds from the nominal center, and (u,v) are in fractions of a pupil from the nominal center.

To use the code to generate lookup tables:

from fieldSteer import *
mp = genPTable()
mc = genCTable()

fieldSteer.calibrate()

define the mirrors and nominal angles of the system.

fieldSteer.genPTable(limit=0.005, delta=None)

generate a lookup table for pointing motions

fieldSteer.genCTable(limit=0.01, delta=None)

generate a lookup table for centering motions

fieldSteer.point(pxa, pya, verbose=False, sendCommand=False)

calculate the motor positions, A,B,C,D in motor encoder counts, required to point to a given field position, pxa, pya, given in arcseconds.

This is an absolute move. The global p state is set to (pxa,pya)

fieldSteer.center(cxa, cya, verbose=False, sendCommand=False)

calculate the motor positions, A,B,C,D in motor encoder counts, required to center to a given pupil position, cxa, cya, given in fractions of a pupil diameter

This is an absolute move. The global c state is set to (cxa,cya)

fieldSteer.pnc(pxa, pya, cxa, cya, verbose=False, sendCommand=False)

calculate the motor positions, A,B,C,D in motor encoder counts, required to both point and center to a given position, pxa, pya, in arcsec on the focal plane and centring, cxa, cya, in fractions of pupil

fieldSteer.deltaP(dpx, dpy, verbose=False, sendCommand=False)

adjust the pointing by a delta amount, dpx, dpy, given in arcseconds

This updates the global ‘state’ which is p=(0,0), c=(0,0) initially and reset on an absolute move.

fieldSteer.deltaC(dcx, dcy, verbose=False, sendCommand=False)

adjust the centering by a delta amount, dcx, dxy, given in fractions of a pupil

This updates the global ‘state’ which is p=(0,0), c=(0,0) initially and reset on an absolute move.

fieldSteer.command(c, test=False)

send the calculsted motor moves to the motor dispatcher. This command ‘connects’ the pointing and centering calculations to the actual motor controllers, for example:

command(point(x,y))
command(center(u,v))

The order of the c matrix is:

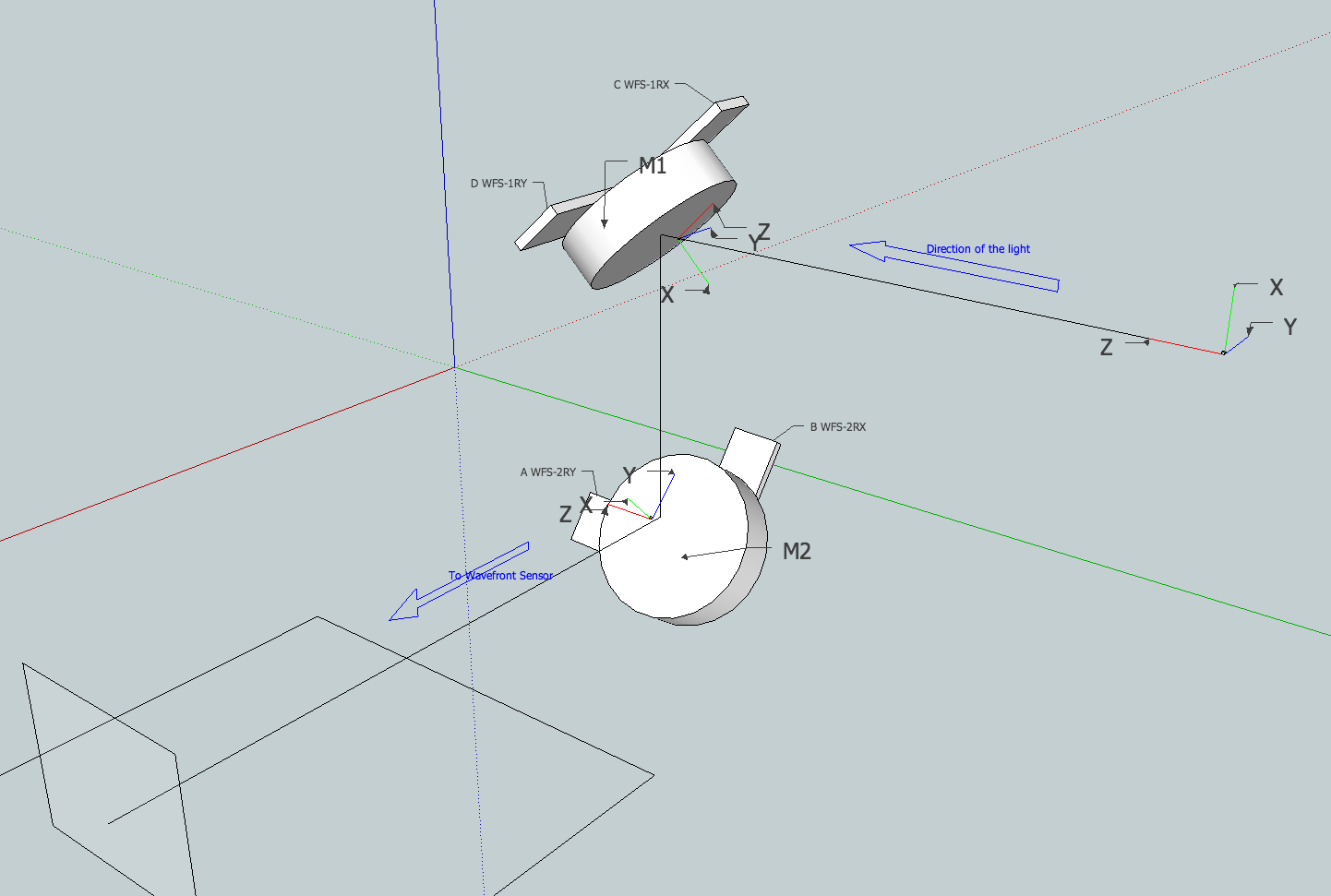
[[ 1Rx, 1Ry],[2rx, 2ry]] = [[C,D],[B,A]]

Module Data

fieldSteer.state = {'p': (0, 0), 'c': (0, 0), 'motors': array([[-40696., -23124.], [-38766., -32791.]])}

global variable for absolute pointing and centering position

Graphics of Field Steer

Figure 1 Sketch of mirror-fixed coordinates rotated with respect to origin coordinates into their nominal positions.

Figure 2 Photograph of the field-steering pair, top-down looing on to bench.

Figure 3 Three-D rendition showing beam line and mirror and motor numbering.

Expert (Low-Level) Use

The fieldSteer module uses linear algebra transformations to implement Euler rotations, intersections, and ray tracing. Here are more internal functions that support this.

fieldSteer.cross(v, w=None)

cross product of 2 3-vectors

fieldSteer.euler_rotate(v, w, theta=1.0)

general rotation of the vector(s) v about an arbitrary vector w, by an amount theta

fieldSteer.intersect(ray, plane)

Intersect a ray with a plane mirror ray = tuple (position, direction) both 3-vectors, or direction can be a matrix whose columns are 3-vectors in which case the 3ed column is treated as the ray direction plane = tuple (position, normal) both 3-vectors

fieldSteer.normalized(v)

return the normalized version of a vector

fieldSteer.plotTable(m, title='name me', units='radians')

plot the already generated lookup table for pointing motions

fieldSteer.propagate(ray, distance)

Propagate a ray for a distance ray = tuple (position, direction) both 3-vectors, or direction can be a matrix whose columns are 3-vectors in which case the 3ed column is treated as the ray direction distance = scalar distance

fieldSteer.reflect(ray, mirror)

Reflect a ray off a mirror ray = ray tuple (position,direction) both 3-vectors, or direction can be a matrix whose columns are 3-vectors The vectors are all treated as directions. The position is unchanged mirror = mirror tuple (position, normal) both 3-vectors, or a normalized 3-vector

It is implicitly assumed that the ray position is a point on the mirror plane, but this is not checked.

fieldSteer.rotate(dir, alpha)

return the active rotation matrix about an axis dir = ‘x’, ‘y’, or ‘z’ alpha = angle, in radians

fieldSteer.shoot(r, m1=(0.0, 0.0), m2=(0.0, 0.0))

Shoots a ray starting at point r (and telecentric direction z) to the focal plane. argument r is a 3-vector

m1 and m2 are optional commands that move the two steering mirrors. the command is given as two angles, (ra, rb) in radians. The ra and rb axes are afixed to each mirror and orthogonal to the mirror’s normal, as defined in the calibration.

returns (position,rotation matrix) = tuple(3-vector,3x3 matrix) denoting the ray as it hit focal plane,

expressed in focal plane coordinates

The intercept point is the first element of the returned tuple The intercept angle is encoded in the z-vector (3ed column) of the second element of the returned tuple

fieldSteer.pshoot(m1, m2, relative=False, verbose=False)

pea-shoot: do a dead reckoning command of the four motors and find out where the beam ends up. Input is the 4 motor commands, in encoder counts, given as 2 2-tuples corresponding to motors (C,D),(A,B) or (WFS1RX, WFS1RY),(WFS2RY,WFS2RX) The input can be relative to the nominal aligned position if the keyword relative=True. Output is position on the focal plane (x,y) in mm, and angle on the focal plane (x,y) in fractions of a pupil diameter.

fieldSteer.vector(l)

create a column vector given a list

fieldSteer.drawPlot(kind)

plot the various motion results.

Pointing is shown on the focal plane, in focal plane coordinates. Units are meters, and generally shown on a +/- 10mm scale

Centering is shown on the focal plane as an incident angle at the focal plane. Units are radians, generally shown on a +/- 10mr scale The pupil diameter is ~50mr (=1/f#)

Raw Motion: +/- 30 milliradian of motion of each mirror channel in turn.

Linear Solved: Computes the sensitivity of p and c to mirror motions (see Rmatrix), using deltas of 1 mr mirror commands Then ‘solves’ for the mirror commands using the inverse of this matrix as desired position is scanned from -3 to +3 mm

Experimental Motion: A ‘hand waving’ argument that non-decentering pointing moves are coordinated motions of the mirror motors related by a factor of sqrt(2) and axes are independent. The mirror1 is scanned +/- 60 mr in each axis, with mirror2 following according to the scale factor.

Optimizer: A least-squares solution to the motor moves that produce non-decentering position moves. The desired positions are scanned +/- 5mm. Two additional plots show the mirror commands that do this.

Calibration Data

The fieldSteer module must be properly calibrated with empirical data in order to do proper predictions of beam motion. Here are the calibration parameters and their current default settings

fieldSteer.d12 = 0.035

distance, m1 -> m2 (meters)

fieldSteer.d23 = 0.08700000000000001

distance, m2 -> focus (meters)

fieldSteer.plate_scale = 0.31

plate scale, mm per arcsecond

fieldSteer.fov_arcsec = 20

field of view, arcseconds on sky

fieldSteer.f_number = 21.0

f/number going into WFS